Preuve de l'irrationalité de e
Prenons tout d’abord e comme étant la sommation suivante :
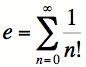
Effectuons une preuve par l’absurde.
Supposons a et b, deux entiers tel que
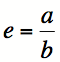 . De plus, a est strictement positif et b est strictement supérieur à 1.
. De plus, a est strictement positif et b est strictement supérieur à 1.Par un artifice de calcul, nous posons la valeur x suivante :
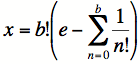
Nous allons montrer que x est un entier strictement positif et plus petit que 1. Cette contradiction établira l’irrationalité de e.
D’abord, montrons que x est un entier :
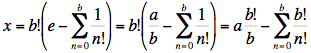
La première égalité est la retranscription de la définition de x établie précédemment. La deuxième égalité présente le e comme étant défini par l’hypothèse (si e est bien rationnel). La troisième égalité montre la distribution de b! dans la parenthèse.
Puisque b divise b! et que pour tout entier n compris entre 0 et b, n! divise b!,
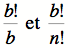 sont des entiers, donc
sont des entiers, donc 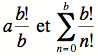 sont aussi des entiers et leur différence est de même. Le x est bel et bien un entier.
sont aussi des entiers et leur différence est de même. Le x est bel et bien un entier.Ensuite, montrons que x est strictement positif et qu’il est plus petit que un :
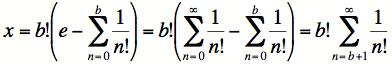
La première égalité est la définition même de x. La deuxième égalité change e pour sa première définition donnée dans cette section. La troisième égalité a simplifié la parenthèse en effectuant la soustraction.
Ainsi, en développant cette dernière égalité (qui est bien sur positive puisqu’il s’agit d’une sommation n’impliquant que des nombres positifs) nous obtenons :
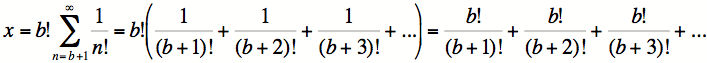
Or, nous savons que cette sommation est positive, puisqu’elle n’est constituée que de termes positifs. En la simplifiant, nous obtenons :
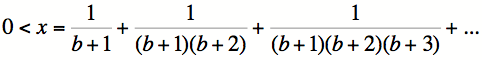
Cette sommation est évidemment plus petite que
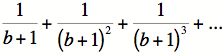 qui est une suite géométrique dont la raison est
qui est une suite géométrique dont la raison est 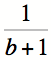 et qui est égale à
et qui est égale à  . Par hypothèse,
. Par hypothèse, 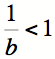 et donc x est plus petit que 1.
et donc x est plus petit que 1. Puisqu’il n’existe aucun entier strictement positif plus petit que un, il y a une contradiction. Donc, e est un nombre irrationnel.
CQFD (ce qu'il fallait démontrer).
Il existe bien sur d’autres preuves de l’irrationalité du nombre e, mais celle-ci est, à notre avis, la plus simple à expliquer et à comprendre.

