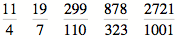Curiosités liées au nombre e
Bernouilli et la spirale logarithmique
Le mathématicien suisse Jacques Bernouilli, qui a découvert le nombre e par son calcul des intérêts composés, était fasciné par les applications de ce nombre au tracé des courbes polaires. Il s’intéressait particulièrement aux spirales logarithmiques, définies en coordonnées polaires par une équation du type
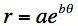 .
. 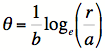 .
. Le plus amusant c’est que Bernouilli exigea dans son testament qu’une telle spirale fût tracée sur sa pierre tombale à côté de l’inscription « Changé en moi-même, je renais. » Une spirale fût bel et bien gravée sur la tombe de Bernouilli à sa mort, mais le graveur a commis toute une bévue en inscrivant non pas une spirale logarithmique, mais une spirale d’Archimède!
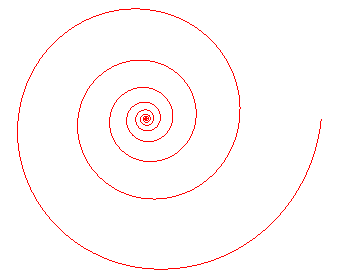

Spirale logarithmique Spirale d’Archimède figurant sur la
tombe de Bernouilli
Comme le montre ces images, la spirale d’Archimède a toujours la même distance entre chacune de ses spires, alors que pour la spirale logarithmique, cette distance augmente de spire en spire.
Autre fait intéressant à propos de la spirale logarithmique, c’est qu’on l’observe telle quelle dans différents objets de la nature. Comme le montre ces images, une coquille d’escargot présente exactement cette forme, tout comme la disposition des graines d’un tournesol. Les amas de nuages de certaines dépressions ont déjà formé des spirales logarithmiques, tout comme certaines galaxies à des années-lumière d’ici! Fascinant non?




Google et le nombre e
En 2004, l’entreprise qui dirige le plus célèbre moteur de recherche sur Internet, Google, a fait une annonce très singulière concernant les fonds à amasser pour se développer. Au lieu d’annoncer un « chiffre rond », comme le veut l’expression populaire, comme un ou deux milliards de dollars, la compagnie proposa un montant de 2 718 281 828 dollars. Pourquoi un nombre aussi précis? Espérons que vous avez reconnu le nombre e, car il s’agissait effectivement d’une blague s’adressant à la communauté des mathématiciens, qui eux connaissent très bien ce nombre!
D’ailleurs, dans les mois qui suivirent, Google allait se servir de e dans le but de sélectionner de brillants mathématiciens pour faire fonctionner son entreprise. Partout aux États-Unis, des panneaux publicitaires affichaient :
(premier nombre premier à dix chiffres trouvé dans les décimales de e qui se suivent).com
En se rendant sur le site internet, les rares qui possédaient les habiletés pour percer cette énigme se retrouvaient devant un autre problème, encore plus épineux. Après avoir résolu plusieurs questions de ce genre, les érudits aboutissaient à une page Internet leur offrant un emploi chez Google, leurs incroyables habiletés mathématiques ayant servi d’entrevue de sélection!
(Cette anecdote figure aussi dans le Livre des nombres de Peter J. Bentley.)
Blague sur le nombre e
Dans une petite soirée, différentes fonctions se rencontrent pour échanger et s'amuser. Elles semblent toutes avoir beaucoup de plaisir et prendre part aux nombreuses activités, sauf une. Sin(x) le remarque et va donc lui en parler :
Sin(x) : "Hey
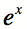 , pourquoi est-ce que tu restes dans ton coin?"
, pourquoi est-ce que tu restes dans ton coin?"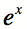 : "J'ai beau essayer de parler aux autres, que je m'intègre ou non, ça ne change jamais rien..."
: "J'ai beau essayer de parler aux autres, que je m'intègre ou non, ça ne change jamais rien..."(Pour des détails, voir la section Le nombre e au niveau collégial.)
Identité d'Euler
La relation mathématique suivante a été nommée ainsi en l'honneur du célèbre mathématicien Léonard Euler.
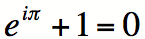
Cette identité a fasciné de nombreux mathématiciens, car elle relie les nombres qui ont suscité le plus d'émoi et de discussions dans l'histoire des mathématiques.
D'ailleurs, dans la préface de l'un de ses cahiers, Richard Feynman, l'un des physiciens les plus influent de la seconde moitié du vingtième siècle, a qualifié cette identité de la "formule la plus remarquable du monde".
Richard Feynman, The Feynman Lectures on Physics: Volume I, juin 1970, p.10 p., « Chapter 22: Algebra »
Un lien entre e, π et φ
Ces trois constantes irrationnelles ont intrigué des générations de mathématiciens. Il est amusant de constater qu'avec π et φ il est possible d'obtenir une bonne approximation de e à trois décimales près.
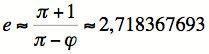
où
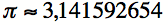 et
et 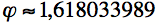
D'autres fractions intéressantes
Plusieurs mathématiciens ont tenté de trouver des fractions offrant une bonne approximation du nombre e. En voici quelques-unes qui permettent respectivement des précisions de une, deux, trois, quatre et cinq décimales :