Activité permettant d'approximer e
Voici un exemple d’activité visant l’introduction de la notion d’intérêts composés et de ses limites.
Imaginons qu’un grand-oncle éloigné vient de mourir subitement. Après avoir surmonté votre immense chagrin, un notaire vous appelle pour vous informer que ce vieil oncle que vous ne connaissiez pas vraiment vous a légué une belle somme d’argent, soit 15 000$. Vous décidez de le placer quelques temps à la banque pour ne l’utiliser que lorsque vous en aurez vraiment besoin. Vous allez donc rencontrer votre banquier pour discuter du placement qui pourrait vous convenir. Le banquier vous propose trois plans de placement différents :
Plan A : Placer le montant à un taux d’intérêt annuel de 6%, composé une fois par année ;
Plan B : Placer le montant à un taux d’intérêt annuel de 6%, composé deux fois par année ;
Plan C : Placer le montant à un taux d’intérêt annuel de 6%, composé six fois par année ;
Pour voir plus clairement la différence entre ces placements, remplissez le tableau suivant :
Premier tableau
a) Selon vous, quel placement est le plus avantageux ?
b) Pour un même taux d’intérêt annuel, que pourriez-vous faire pour avoir encore plus d’argent après chaque année ?
c) Selon vous, y a-t-il une limite à la composition d’intérêts ? Si oui, quelle est-elle ?
Pour vous aider à répondre à la question c), voici un autre tableau à remplir. Imaginez un placement de 1$ à un taux d’intérêt annuel de 100%.
Deuxième tableau *
d) Est-ce que le montant continue à augmenter selon le nombre de périodes par année ou semble-t-il stagner à une valeur précise ?
e) Appuyez sur la touche
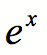de votre calculatrice et calculez 
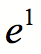. Que remarquez-vous ?Remarquez que si vous aviez voulu calculer votre placement initial à un taux d’intérêt annuel de 6% calculé de manière continue, l’équation à utiliser aurait été :
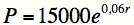
où P est la valeur du placement ($) et r le nombre d’années.
Réponses de l’activité
Premier tableau corrigé
r : nombre d’années
De manière plus générale encore, pour un nombre r d’années, si le calcul est fait n fois durant l’année, pour un investissement initial de a dollars à un taux d’intérêt annuel i, la formule pour calculer la valeur du placement P sera :
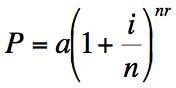
a) Selon vous, quel placement est le plus avantageux ?
Le placement le plus avantageux est le placement C, donc celui dont les intérêts sont composés 6 fois durant l’année.
b) Pour un même taux d’intérêt annuel, que pourriez-vous faire pour avoir encore plus d’argent après chaque année ?
Faire composer les intérêts encore plus souvent durant l’année (voire de manière continue, donc une infinité de fois)
c) Selon vous, y a-t-il une limite à la composition d’intérêts ? Si oui, quelle est-elle ?
Réponse attendue des élèves : Non, il n’y a pas de limite.
Animer une petite discussion à ce sujet en laissant les élèves exprimer leurs idées.
Deuxième tableau corrigé
d) Est-ce que le montant continue à augmenter selon le nombre de périodes par année ou semble-t-il stagner à une valeur précise ?
Il semble tendre vers une valeur.
e) Appuyez sur la touche
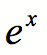de votre calculatrice et calculez 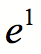. Que remarquez-vous ?Cela ressemble beaucoup au nombre trouvé à la dernière colonne du tableau.
* Note sur le tableau 2 de l'activité
Il est possible d'utiliser un fichier Excel pour calculer l'approximation de e présentée dans le deuxième tableau de cette activité. Par contre, le résultat obtenu ne sera pas concluant pour approximer e. En effet, même si nous augmentons considérablement la valeur de n utilisée dans le calcul, cette valeur fournit une précision à 4 décimales avec n = 65534. Il est possible de continuer de calculer encore, mais il faut de plus en plus d'opérations pour obtenir de nouvelles décimales exactes.
Par ailleurs, toujours sur Excel, il est possible d'obtenir une meilleure approximation en utilisant la définition de e en série telle qu'énoncée par Euler (voir Historique du nombre e). Déjà, lorsque n = 17, on obtient à précision de 14 décimales, ce qui est nettement plus efficace qu'avec la méthode précédente. Toutefois, lorsque n = 171, le calcul demandé dépasse la capacité d'Excel et il est alors impossible d'afficher le résultat pour cette valeur ou une valeur plus grande de n.
C'est pour ces raisons que nous suggérons fortement l'utilisation de la calculatrice graphique pour cette activité.
Voici un fichier Excel qui illustre ce propos :
Approximation de e - Excel