Les visions de l'univers (Cosmographie et astronomie) :
Ptolémée (v.90 - v.168)
(À moins d'avis contraire, les figures proviennent de Thomas S. Kuhn, The Copernician Revolution, Planetary Astronomy in the Development of Western Thought, Harvard Un. Press, 1957.)
Mouvements apparents des planètes.
-
Sept étoiles mobiles : les planètes
En examinant quotidiennement la voûte étoilée, on remarque 7 'étoiles' qui changent progressivement de position par rapport aux autres étoiles fixes. Ces 'étoiles' sont le Soleil, la Lune, Mercure, Vénus, Mars, Jupiter, Saturne.
-
Les orbites des planètes sont toutes approximativement dans le même plan
Les planètes ne s'éloignent jamais de plus de 8° de l'écliptique (zodiaque).
-
Les temps de translation varient, mais ils sont en moyenne constants
Chaque planète parcourt le zodiaque en entier en un temps qui lui est propre. L'intervalle de temps mis par une planète pour revenir à une position donnée varie d'une fois à l'autre de façon presque imprévisible. Par ailleurs, la moyenne de ces intervalles de temps (temps de translation) est constante (Exemple : En moyenne, la lune revient à un même point du zodiaque tous les 29 1/3 jours, mais le temps entre chaque retour peut varier jusqu'à 7h. de cette moyenne en plus ou moins).
-
Les planètes inférieures: Mercure et Vénus
Mercure et Vénus ne s'éloignent jamais beaucoup du Soleil.
-
Le mouvement de rétrogradation des planètes
Les mouvements apparents des planètes, sauf ceux du Soleil et de la Lune, sont entachés d'une autre irrégularité, la rétrogradation.
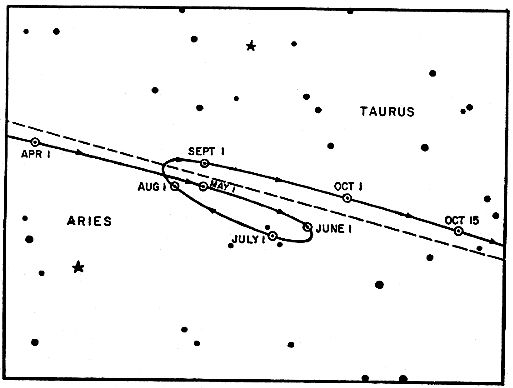
a) Les rétrogradations se font à des intervalles à peu près réguliers, mais pas toujours aux mêmes endroits dans le ciel.
b) Pour les planètes Mars, Jupiter et Saturne, elles se font lorsque
i) la planète est en opposition avec le Soleil (donc la planète, la Terre et le Soleil sont alignés, dans cet ordre),
ii) l'intensité lumineuse de la planète est alors à son maximum. Donc on peut croire qu'elle est plus près de la Terre qu'à d'autres moments.
Le modèle ptoléméen : Description du modèle
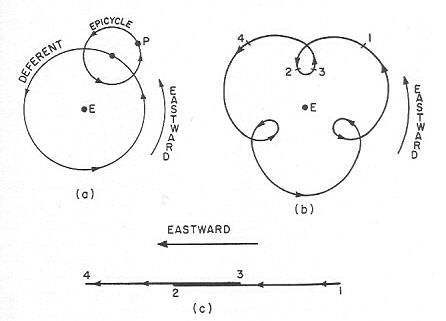
Le modèle de Ptolémée ne concerne véritablement que les planètes et le Soleil. En ce qui a trait aux étoiles, il s'en tient au modèle des deux sphères. Pour décrire le mouvement des planètes, il a recours à la combinaison à deux mouvements circulaires, s'inspirant en cela des travaux, aujourd'hui perdus, de l'astronome Hipparque (v. 190, v.-120). Chaque planète est située sur un petit cercle, appelé épicycle, dont le centre est lui-même placé sur autre cercle, appelé déférent, centré près du centre de l'univers. Idéalement, les deux cercles ont chacun une vitesse angulaire constante. Selon les rapports des vitesses angulaires des deux cercles et selon les rapports des rayons des cercles, la planète décrira une trajectoire particulière. Dans la figure ci-dessous, l'épicycle tourne à une vitesse angulaire trois fois plus grande que la vitesse angulaire du déférent.
Les deux vidéos suivantes nous donnent une idée de la façon dont Hipparque et Ptolémée conçoivent les mouvements possibles des planètes :
-
Les épicycles d'Hipparque (1minute 52 secondes) -- Les ajustements de Ptolémée (41 secondes)
--
Ces vidéos proviennent du FSM
3000 (sur internet) de l'UQAM.
Ptolémée est assez clair sur les objectifs qu'il s'est donnés:
Nous croyons que le but que l'astronome doit s'efforcer d'atteindre est le suivant : démontrer que tous les phénomènes du ciel sont produits par des mouvements circulaires et uniformes. (... ) Nous étant fixé la tâche de prouver que les irrégularités apparentes des cinq planètes, du Soleil et de la Lune peuvent être toutes représentées au moyen de mouvements circulaires uniformes, parce que seuls ces mouvements sont appropriés à leur nature divine... nous sommes en droit de regarder l'accomplissement de cette tâche comme le but ultime de la science mathématique basée sur la philosophie.
L'on voit donc que Ptolémée fait sienne la dichotomie entre le monde terrestre et le monde céleste. L'influence platonicienne et aristotélicienne est claire. Aristote lui donne la structure globale du monde. Platon lui donne la justification de traiter purement idéalement les planètes. Il n'y a pas de lois de la physique impliquées ici. Les êtres célestes font partie du monde des idées. Nous pouvons tenter des connaître par la géométrie leurs déplacements. Mais leur nature nous demeure inaccessible.